Многоэкстремальные задачи
- Многоэкстремальные задачи
-
Многоэкстремальные задачи [multi-extremality problems] — нелинейные задачи математического программирования, целевая функция которых может иметь как глобальный, так и локальные оптимумы. Такие задачи очень сложны для решения. Причину этого можно объяснить на следующем упрощенном примере (рис. M.3).
Функция y=f(x), изображенная жирной линией, — многоэкстремальна. Если двигаться по кривой от точки x1 к точке x2 (и не знать при этом дальнейшей формы кривой), то можно x2 принять за оптимальное значение переменной x: анализ покажет, что достигнут максимум функции f(x): первая производная функции в этой точке равна нулю, а вторая — отрицательна. Между тем, глобальный оптимум находится лишь в точке x3.
В М.з. соответственно существуют такие допустимые наборы значений управляющих параметров (инструментальных переменных), которые являются наилучшими среди достаточно близких к ним наборов, но тем не менее не оптимальными.
Один из реальных подходов к решению М.з. состоит в том, что какими-то дополнительными приемами кривая f(x) сглаживается и задача приводится к одноэкстремальной задаче программирования (см. на рис. M.3 пунктирную линию). Термин «М.з.» иногда смешивают с терминами «Векторные задачи» и «Многокритериальные задачи». Это неправильно по причинам, объясненным в ст. Многокритериальная оптимизация.
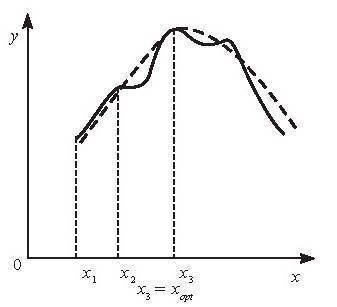
Рис . М.3 Многоэкстремальная функция одного переменного (x1 = xopt)
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело.
Л. И. Лопатников.
2003.
Полезное
Смотреть что такое "Многоэкстремальные задачи" в других словарях:
многоэкстремальные задачи — Нелинейные задачи математического программирования, целевая функция которых может иметь как глобальный, так и локальные оптимумы. Такие задачи очень сложны для решения. Причину этого можно объяснить на следующем упрощенном примере (рис. M.3).… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ — математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). М. п.… … Математическая энциклопедия
Математическое программирование — математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). М. п. раздел науки об… … Большая советская энциклопедия
Нелинейное программирование — [nonlinear programming] раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями. В экономике это соответствует … Экономико-математический словарь
нелинейное программирование — Раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями. В экономике это соответствует тому, что результаты… … Справочник технического переводчика
Многокритериальная оптимизация — [multi criterion optimization] 1. Метод решения задач, которые состоят в поиске лучшего (оптимального) решения, удовлетворяющего нескольким несводимым друг к другу критериям. 2. Соответствующий раздел математического программирования. Например,… … Экономико-математический словарь
многокритериальная оптимизация — 1. Метод решения задач, которые состоят в поиске лучшего (оптимального) решения, удовлетворяющего нескольким несводимым друг к другу критериям. 2. Соответствующий раздел математического программирования. Например, надо принять решение о постройке … Справочник технического переводчика
М — Магистраль [turnpike] Мажоритарный акционер (Majority shareholder) Мажоритарная доля собственности (majority interest) Мажоритарный контроль (majority control) … Экономико-математический словарь

